Swiftpack.co is a collection of thousands of indexed Swift packages. Search packages.
See all packages published by indisoluble.
indisoluble/SwiftQuantumComputing 26.1.0
Quantum circuit simulator in Swift
⭐️ 41
🕓 2 years ago
iOS
macOS
.package(url: "https://github.com/indisoluble/SwiftQuantumComputing.git", from: "26.1.0")
Quantum circuit simulator in Swift
Usage
Circuit
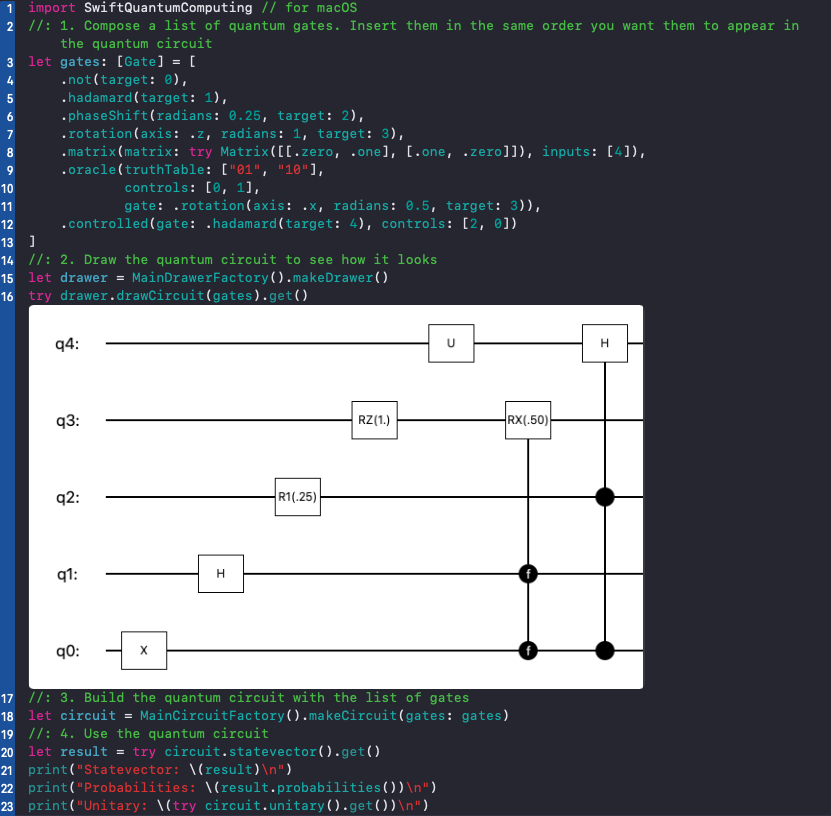
Check code in Circuit.playground.
Circuit with noise
import SwiftQuantumComputing // for macOS
//: 1. Compose a list of quantum gates & noises
let quantumOperators: [QuantumOperatorConvertible] = [
Gate.hadamard(target: 0),
Noise.bitFlip(probability: 0.35, target: 0),
Gate.phaseShift(radians: 0.25, target: 2),
Noise.phaseDamping(probability: 0.75, target: 2),
Gate.controlled(gate: .hadamard(target: 1), controls: [2, 0]),
Noise.bitFlip(probability: 0.8, target: 1)
]
//: 2. Build a quantum circuit with noise using the list
let circuit = MainNoiseCircuitFactory().makeNoiseCircuit(quantumOperators: quantumOperators)
//: 3. Use the quantum circuit with noise
let result = try circuit.densityMatrix().get()
print("Density matrix: \(result)\n")
print("Probabilities: \(result.probabilities())\n")
Check code in NoiseCircuit.playground.
Performance
~/SwiftQuantumComputing % swift run sqc-measure-performance
Run this application to check the performance of this simulator in your computer. Execute swift run sqc-measure-performance -h to see all available options.
Check code in SQCMeasurePerformance/main.swift.
Algorithms
- Use a genetic algorithm to automatically generate a quantum circuit - Check example in Genetic.playground.
- Two-level decomposition: Decompose any gate into an equivalent sequence of not gates and fully controlled phase shifts, z-rotations, y-rotations & not gates - Check example in TwoLevelDecomposition.playground.
Other algorithms
- Euclidean Algorithm: Find greatest common divisor of two integers - Check example in EuclideanAlgorithm.playground.
- Continued Fractions: Find an approximation to a given rational number - Check example in ContinuedFractions.playground.
- Gaussian Elimination: Solve a system of XOR equations - Check example in XorGaussianElimination.playground.
More examples
- Bernstein–Vazirani algorithm - Check code in BernsteinVaziraniAlgorithm.playground.
- Deutsch's algorithm - Check code in DeutschAlgorithm.playground.
- Deutsch-Jozsa algorithm - Check code in DeutschJozsaAlgorithm.playground.
- Grover's algorithm - Check code in GroverAlgorithm.playground.
- Shor's Algorithm - Check code in ShorAlgorithm.playground.
- Simon's periodicity algorithm - Check code in SimonPeriodicityAlgorithm.playground.
Documentation
Documentation for the project can be found here.
References
- Amazon Braket Default Simulator
- Automatic Quantum Computer Programming: A Genetic Programming Approach
- Continued Fractions and the Euclidean Algorithm
- Decomposition of unitary matrices and quantum gates
- Decomposition of unitary matrix into quantum gates
- IBM Qiskit
- qHiPSTER: The Quantum High Performance Software Testing Environment
- Quantum Computing for Computer Scientists
- Shor's Quantum Factoring Algorithm
SwiftPM dependencies
- CBLAS-Linux (only for Linux)
- CLapacke-Linux (only for Linux)
- Swift Argument Parser
- Swift Numerics
Linux
This package depends on BLAS & LAPACK if running on Linux, more exactly, Ubuntu.
These dependencies are reflected in Package.swift with:
- CBLAS-Linux, which in turn expects to find:
/usr/include/x86_64-linux-gnu/cblas-netlib.h - CLapacke-Linux, which in turn expects to find:
/usr/include/lapacke.h
So, after installing BLAS & LAPACK (in case they are not already there):
sudo apt-get install libblas-dev liblapacke-dev
Check cblas-netlib.h & lapacke.h are in the expected locations.
GitHub
| link |
| Stars: 41 |
| Last commit: 2 years ago |
Advertisement: IndiePitcher.com - Cold Email Software for Startups
Swiftpack is being maintained by Petr Pavlik | @ptrpavlik | @swiftpackco | API | Analytics
