SwiftNodes

     

👩🏻‍🚀 This project is still a tad experimental. Contributors and pioneers welcome!

What?

SwiftNodes provides a concurrency safe graph data structure together with graph algorithms. A graph stores values in identifiable nodes which can be connected via edges.

Contents

• Why?
• How?
• Included Algorithms
• Architecture
• Development Status
• Roadmap

Why?

Graphs may be the most fundamental mathematical concept besides numbers. They have wide applications in problem solving, data analysis and visualization. And although such data structures fit well with the language, graph implementations in Swift are lacking – in particular, comprehensive graph algorithm libraries.

SwiftNodes was extracted from Codeface, so the current selection of included algorithms stems from there. But SwiftNodes is general enough to serve other applications as well – and extensible enough for more algorithms to be added.

Design Goals

• Usability, safety, extensibility and maintainability – which also imply simplicity.
• In particular, the API is supposed to feel familiar and fit well with official Swift data structures. So one question that guides its design is: What would Apple do?

We put the above qualities over performance. But that doesn't mean we neccessarily end up with suboptimal performance. The main compromise SwiftNodes involves is that nodes are value types and can not be referenced, so they must be hashed. But that doesn't change the average case complexity and, in the future, we might even be able to avoid that hashing in essential use cases by exploiting array indices and accepting lower sorting performance.

How?

The following explanations touch only parts of the SwiftNodes API. We recommend exploring the DocC reference, unit tests and production code. The code in particular is actually small and easy to grasp.

Insert Values

A Graph<NodeID: Hashable, NodeValue> holds values of type NodeValue in nodes of type GraphNode<NodeID: Hashable, NodeValue>. Nodes are unique and have IDs of type NodeID:

var graph = Graph<String, Int> { "id\($0)" }  // NodeID == String, NodeValue == Int
let node = graph.insert(1)                    // node.id == "id1", node.value == 1

let nodeForID1 = graph.node(for: "id1")       // nodeForID1.id == "id1"
let valueForID1 = graph.value(for: "id1")     // valueForID1 == 1

When inserting a value, a Graph must know how to generate the ID of the node that would store the value. So the Graph initializer takes a closure returning a NodeID given a NodeValue.

Side Note: The reason, there's an explicit node type at all is that a) values don't need to be unique, but nodes in a graph are, and b) a node holds caches for quick access to its neighbours. The reason there is an explicit edge type at all is that edges have a count (they are "weighted") and may hold their own values in the future.

Generate Node IDs

You may generate NodeIDs independent of NodeValues:

var graph = Graph<UUID, Int> { _ in UUID() }  // NodeID == UUID, NodeValue == Int
let node1 = graph.insert(42)
let node2 = graph.insert(42)  // node1.id != node2.id, same value in different nodes

If NodeID and NodeValue are the same type, you can omit the closure and the Graph will assume the value is itself used as the node ID:

var graph = Graph<Int, Int>()  // NodeID == NodeValue == Int
let node1 = graph.insert(42)   // node1.value == node1.id == 42
let node2 = graph.insert(42)   // node1.id == node2.id because 42 implies the same ID

And if your NodeValue is itself Identifiable by IDs of type NodeID, then you can also omit the closure and Graph will use the ID of a NodeValue as the NodeID of the node holding that value:

struct IdentifiableValue: Identifiable { let id = UUID() }
var graph = Graph<UUID, IdentifiableValue>()  // NodeID == NodeValue.ID == UUID
let node = graph.insert(IdentifiableValue())  // node.id == node.value.id

Connect Nodes via Edges

var graph = Graph<String, Int> { "id\($0)" }
let node1 = graph.insert(1)
let node2 = graph.insert(2)
let edge = graph.addEdge(from: node1.id,  to: node2.id)

An edge is directed and goes from its edge.originID node ID to its edge.destinationID node ID.

Specify Edge Counts

Every edge has an integer count accessible via edge.count. It is more specifically a "count" rather than a "weight", as it increases when the same edge is added again. By default, a new edge has count 1 and adding it again increases its count by 1. But you can specify a custom count when adding an edge:

graph.addEdge(from: node1.id, to: node2.id, count: 40)  // edge count is 40
graph.addEdge(from: node1.id, to: node2.id, count: 2)   // edge count is 42

Remove Edges

A GraphEdge<NodeID: Hashable, NodeValue> has its own ID type which combines the edge's originID- and destinationID node IDs. In the context of a Graph or GraphEdge, you can create edge IDs like so:

let edgeID = Edge.ID(node1.id, node2.id)

This leads to 3 ways of removing an edge:

let edge = graph.addEdge(from: node1.id, to: node2.id)

graph.removeEdge(with: edge.id)
graph.removeEdge(with: .init(node1.id, node2.id))
graph.removeEdge(from: node1.id, to: node2.id)

Query and Traverse a Graph

Graph offers many ways to query its nodes, node IDs, values and edges. Have a look into Graph.swift to see them all. In addition, a GraphNode has caches that enable quick access to its neighbours:

node.descendantIDs  // IDs of all nodes to which there is an edge from node
node.ancestorIDs    // IDs of all nodes from which there is an edge to node
node.neighbourIDs   // all descendant- and ancestor IDs
node.isSink         // whether node has no descendants
node.isSource       // whether node has no ancestors

Sort Nodes

The nodes in a Graph maintain an order. So you can also sort them:

var graph = Graph<Int, Int>()  // NodeID == NodeValue == Int
graph.insert(5)
graph.insert(3)                // graph.values == [5, 3]
graph.sort { $0.id < $1.id }   // graph.values == [3, 5]

Copy and Share a Graph

Like the official Swift data structures, Graph is a pure struct and inherits the benefits of value types:

• You decide on mutability by using var or let.
• You can use a Graph as a @State or @Published variable with SwiftUI.
• You can use property observers like didSet to observe changes in a Graph.
• You can easily copy a whole Graph.

Many algorithms produce a variant of a given graph. Rather than modifying the original graph, SwiftNodes suggests to copy it. You copy a Graph like any other value. But right now, SwiftNodes lets you add and remove only edges – not nodes. So, to create a subgraph with a subset of the nodes of a graph, you can use graph.subGraph(nodeIDs:...):

var graph = Graph<Int, Int>()
	/* then add a bunch of nodes and edges ... */
let subsetOfNodeIDs: Set<Int> = [0, 3, 6, 9, 12]
let subGraph = graph.subGraph(nodeIDs: subsetOfNodeIDs)

A Graph is also Sendable if its value- and id type are. SwiftNodes is thereby ready for the strict concurrency safety of Swift 6. You can safely share Sendable Graph values between actors.

Mark Nodes in Algorithms

Many graph algorithms do associate little intermediate results with individual nodes. The literature often refers to this as "marking" a node. The most prominent example is marking a node as visited while traversing a potentially cyclic graph. Some algorithms write multiple different markings to nodes.

When we made SwiftNodes concurrency safe (to play well with the new Swift concurrency features), we removed the possibility to mark nodes directly, as that had lost its potential for performance optimization. See how the included algorithms now use hashing to associate markings with nodes.

Included Algorithms

SwiftNodes has begun to accumulate some graph algorithms. The following overview also links to Wikipedia articles that explain what the algorithms do. We recommend also exploring them in code.

Components

graph.findComponents() returns multiple sets of node IDs which represent the components of the graph.

Strongly Connected Components

graph.findStronglyConnectedComponents() returns multiple sets of node IDs which represent the strongly connected components of the graph.

Condensation Graph

graph.makeCondensationGraph() creates the condensation graph of the graph, which is the graph in which all strongly connected components of the original graph have been collapsed into single nodes, so the resulting condensation graph is acyclic.

Minimum Equivalent Graph

graph.makeMinimumEquivalentGraph() creates the MEG of the graph. Right now, this only works on acyclic graphs and might even hang or crash on cyclic ones.

Non-Essential Edges

graph.findNonEssentialEdges() returns the IDs of all edges that correspond to edges of the condensation graph which are not in the MEG of the condensation graph. In simpler terms: Non-essential edges are both 1) not in cycles and 2) already implied by other edges – i.e. the reachability (or "path") they describe is already indirectly given by other edges.

Ancestor Counts

graph.findNumberOfNodeAncestors() returns a [(Node, Int)] containing each node of the graph together with its ancestor count. The ancestor count is the number of all (recursive) ancestors of the node. Basically, it's the number of other nodes from which the node can be reached.

This only works on acyclic graphs right now and might return incorrect results for nodes in cycles.

Ancestor counts can serve as a proxy for topological sorting.

Architecture

Here is the architecture (composition and essential dependencies) of the SwiftNodes code folder:

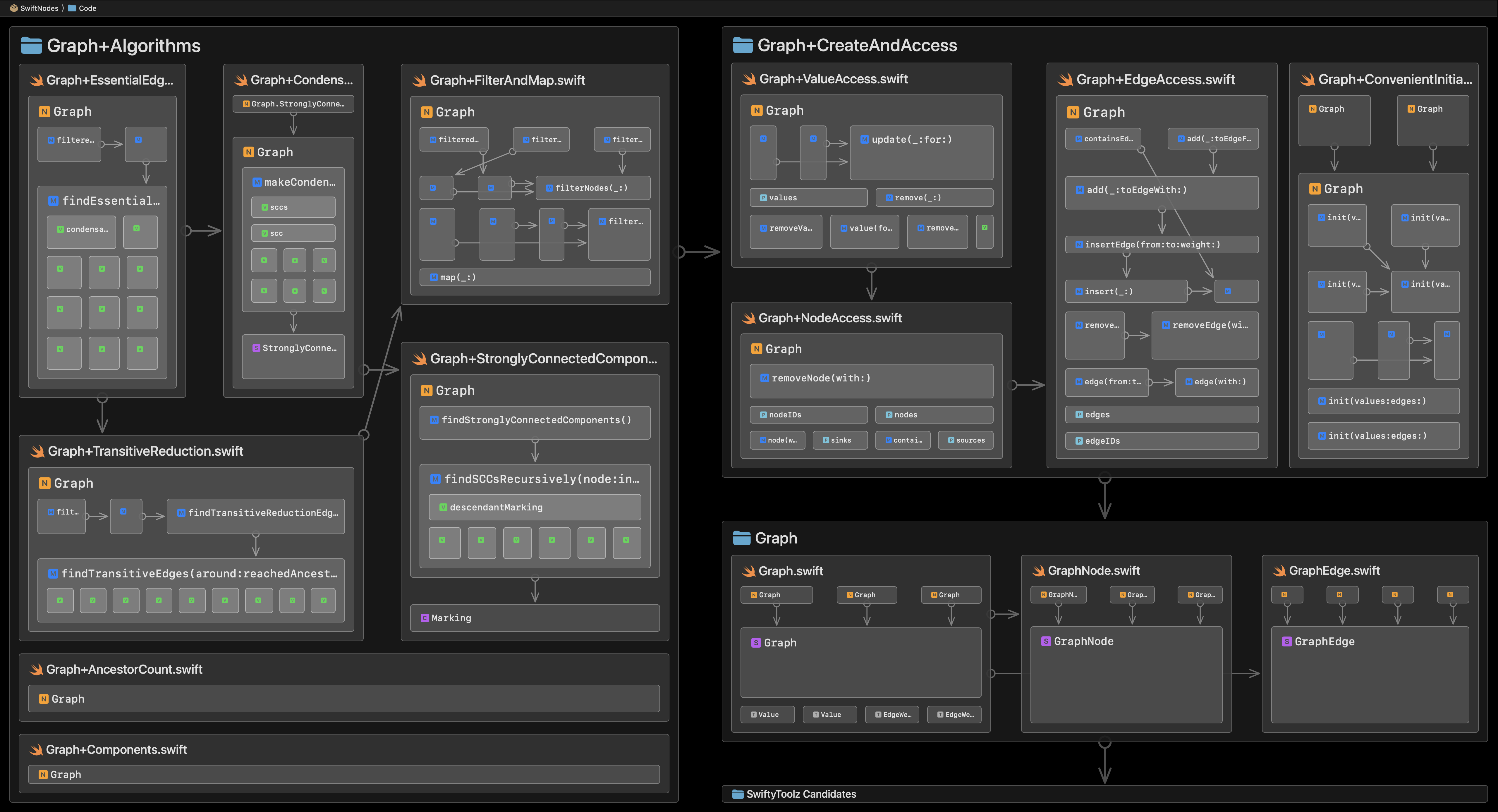
The above image was created with Codeface.

Development Status

From version/tag 0.1.0 on, SwiftNodes adheres to semantic versioning. So until it has reached 1.0.0, its API may still break frequently, and we express those breaks with minor version bumps.

SwiftNodes is already being used in production, but Codeface is still its primary client. SwiftNodes will move to version 1.0.0 as soon as its basic practicality and conceptual soundness have been validated by serving multiple real-world clients.

Roadmap

• For the included algorithms and current clients, existing editing capabilities seem to suffice. Also, to declare a Graph property on a Sendable reference type, you would need to make that property constant anyway. So, development will focus on initializing graphs complete with their edges rather than on mutating existing Graph instances (Add those initializers!).
• Add tests for all algorithms! The test graphs should be complex enough to establish confidence in algorithm correctness.
• Further align with official Swift data structures (What would Apple do?):
  • Align node access with the API of Dictionary (subscripts etc.)
  • Add the usual suspects of applicable protocol conformances (Sequence, Collection, Codable, expressibility by literals, etc.)
  • Add synchronous and asynchronous filtering- and mapping functions. The existing subGraph function should probably rather be some kind of filter over node IDs, unless we employ set operations, or both ...
  • Compare with- and learn from API and implementation of Swift Collections
• Add more algorithms (starting with the needs of Codeface):
  • Make existing algorithms compatible with cyclic graphs (two of them are still not)
  • General purpose graph traversal algorithms (BFT, DFT, compatible with potentially cyclic graphs)
  • Better ways of topological sorting
  • Approximate the minimum feedback arc set, so Codeface can guess "faulty" or unintended dependencies, i.e. the fewest dependencies that need to be cut in order to break all cycles.
• Possibly optimize performance – but only based on measurements and only if measurements show that the optimization yields significant acceleration. Optimizing the algorithms might be more effective than optimizing the data structure itself.